In gear design, the involute is a crucial element that determines the shape of gear teeth. An involute curve is a specific type of curve that is defined by the rolling motion of a line that is tangent to a circle. The curve is widely used in the design of gears because it provides a smooth, uniform meshing action between gears, which reduces noise and wear. In this article, we’ll explore what an involute is and why it’s important in gear design.
What is an Involute Curve?
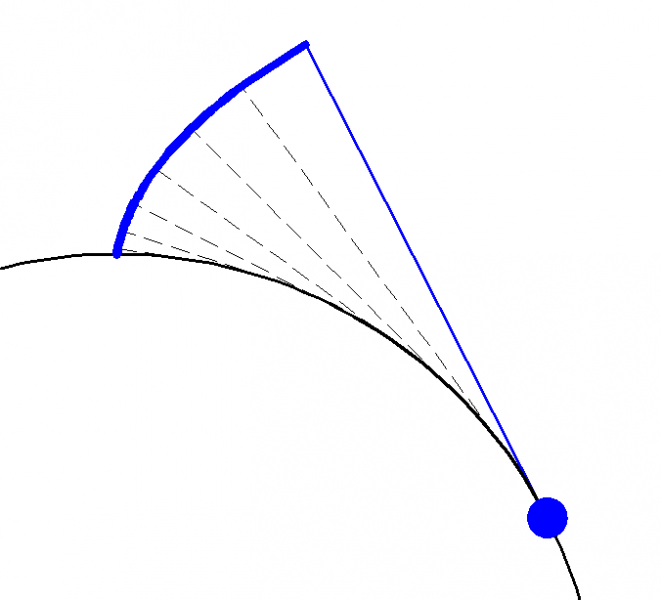
An involute curve is a curve that is traced by a point on a taut string as it is unwound from a stationary circle. The curve is formed by the intersection of the string with a plane that is tangent to the circle. The key feature of the involute curve is that it is self-similar, meaning that its shape remains unchanged when it is scaled up or down. This property is essential in gear design because it allows gear teeth to maintain their shape and meshing properties regardless of their size.
Why is the Involute Important in Gear Design?
The involute curve is critical in gear design because it determines the shape of gear teeth. When two gears mesh, their teeth engage in a rolling motion that is defined by the shape of the involute curve. The curve allows the gears to mesh smoothly and efficiently, minimizing wear and noise. Additionally, the involute curve has a unique property that allows it to maintain a constant speed ratio between gears as they mesh. This property is critical in gear trains where the speed and torque ratios between gears must be precisely controlled.
How is the Involute Used in Gear Design?
In gear design, the involute curve is used to define the shape of gear teeth. The curve is generated by a tool called an involute gear cutter, which cuts the gear teeth from a gear blank. The cutter is designed to generate the correct involute shape for a given module or pitch of the gear. The involute curve is then used to calculate the necessary dimensions for the gear teeth, including the tooth thickness, addendum, dedendum, and clearance.
